REFLEXIÓN SOBRE LA MATERIA ESTRUCTURAS DE PROGRAMACIÓN

La materia para mi fue muy difícil, cada trabajo fue un nuevo desafío y la verdad me constaron bastante.

Considero que la materia es importante y muy útil, aprendí muchas cosas y para mi que no sabía nada de computación fue de gran ayuda para aprender a usar nuevas herramientas.

SABIENDO ALGO SOBRE PITÁGORAS

¿Quién es Pitágoras?

Pitágoras (aprox. 582 a.C. - 507 a.C.) fue un filósofo y matemático griego, nacido en la isla de Samos.
Siendo muy joven, viajó a Mesopotamia y Egipto. Tras regresar a Samos, finalizó sus estudios y fundó su primera escuela.
Abandonó Samos para escapar de la tiranía de Polícrates y se estableció en Crotona en el sur de Italia, donde fundó su segunda escuela.
Sus estudiantes pertenecían a todas las razas, religiones y estratos económicos y sociales. Tras ser expulsados por los pobladores de Crotona, los pitagóricos se exiliaron a Tarento donde fundó su tercera escuela.
Su escuela de pensamiento afirmaba que la estructura del universo era aritmética y geométrica, a partir de lo cual las matemáticas se convirtieron en una disciplina fundamental para toda investigación científica.
Pitágoras pasa por ser el introductor de pesos y medidas, elaborador de la teoría musical; primero en hablar de "teoría" y de "filósofos", en postular el vacío, en canalizar el fervor religioso en fervor intelectual, en usar la definición y en considerar que el universo era una obra sólo descifrable a través de las matemáticas.
Fueron los pitagóricos los primeros en sostener la forma esférica de la tierra y postular que ésta, junto con el sol y el resto de los planetas conocidos, no se encontraban en el centro del universo, sino que giraban entorno de una fuerza simbolizada por el número uno.

LINK DE LA PÁGINA

http://platea.pntic.mec.es/curso20/5_edicionhtml/2007/html11/quien.html

Teorema de Pitágoras

Hace años, un hombre llamado Pitágoras descubrió un hecho asombroso sobre triángulos: Si el triángulo tiene un ángulo recto (90°)... ... y pones un cuadrado sobre cada uno de sus lados, entonces... ... ¡el cuadrado más grande tiene exactamente la misma área que los otros dos cuadrados juntos!

El lado más largo del triángulo se llama "hipotenusa", así que la definición formal es:

En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)

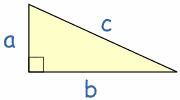Entonces, el cuadrado de a (a²) más el cuadrado de b (b²) es igual al cuadrado de c (c²): a2 + b2 = c2

¿Seguro... ?

Veamos si funciona con un ejemplo. Un triángulo de lados "3,4,5" tiene un ángulo recto, así que la fórmula debería funcionar.

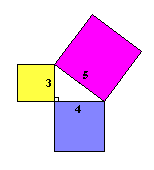Veamos si las áreas son la misma: 32 + 42 = 52 Calculando obtenemos: 9 + 16 = 25 ¡sí, funciona!

¿Por qué es útil esto?

Si sabemos las longitudes de dos lados de un triángulo con un ángulo recto, el Teorema de Pitágoras nos ayuda a encontrar la longitud del tercer lado. (¡Pero recuerda que sólo funciona en triángulos rectángulos!)

¿Cómo lo uso?

Escríbelo como una ecuación:

a2 + b2 = c2

Ahora puedes usar álgebra para encontrar el valor que falta, como en estos ejemplos:

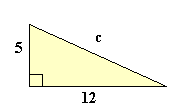
a2 + b2 = c2 52 + 122 = c2 25 + 144 = 169 c2 = 169 c = √169 c = 13

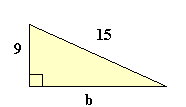
a2 + b2 = c2 92 + b2 = 152 81 + b2 = 225 Resta 81 a ambos lados b2 = 144 b = √144 b = 12

¡Y Puedes Demostrarlo Tú Mismo!

Consigue papel y tijeras, y usa la siguiente animación como guía:
	Dibuja un triángulo rectángulo en el papel, dejando mucho espacio alrededor. Dibuja un cuadrado sobre la hipotenusa (el lado más largo) Dibuja un cuadrado del mismo tamaño en el otro lado de la hipotenusa Dibuja líneas como en la animación, así: Recorta los trozos Colócalos de manera que puedas demostrar que el cuadrado grande tiene la misma área que los cuadrados en los otros lados juntos

Otra Demostración, Muy Simple

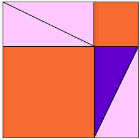
Aquí tienes una de las demostraciones más antiguas de que el cuadrado grande tiene la misma área que los otros cuadrados juntos.
	Mira la animación, y presta atención cuando se empiecen a mover los triángulos. Quizás quieras verla varias veces para entender bien lo que pasa. El triángulo violeta es el importante.

También tenemos una demostración sumando las áreas.

Nota histórica: aunque se llama Teorema de Pitágoras, ¡también lo conocían los matemáticos indios, griegos, chinos y babilonios antes de que él viviera!

LINK DE LA PÁGINA

http://www.disfrutalasmatematicas.com/geometria/teorema-pitagoras.html